
Benjamin R. Bray
I’m a full-stack software engineer currently living in Tokyo, Japan. These days, I’m most interested in working on:
- Language servers, static analyzers, and compilers.
- Interactive editors for composing rich text documents.
- Computer graphics, simulation, and numerical methods.
I most often reach for TypeScript, Rust, or Haskell when starting a new project. In my free time, I enjoy cycling, goats, dodgeball, long walks, and baking. Maybe one day I’ll make more games!
If you’d like to chat, feel free to write me at benrbray@gmail.com.
Selected Projects
A collection of reference implementations of type inference algorithms, with particular emphasis on features which are necessary for practical implementations, such as error reporting.
A collection of plugins for the
remark markdown processor adding support for pandoc-style inline citation syntax and bibliography formatting.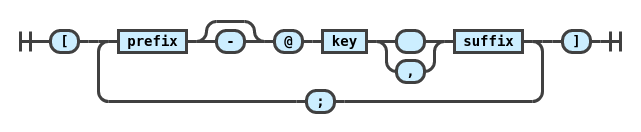
An open-source Markdown editor with bidirectional links and excellent math support!
Schema and plugins for writing mathematics in
prosemirror, using KaTeX.
As an undergraduate research assistant, I spent three years as the primary developer for an NLP-driven web application built to assist a humanities professor with research on 19th-century German literature.

I used linear algebra to give my high school robotics team a competitive edge! Since robots compete in teams of three, an individual's contribution to the final score cannot be known. By scraping public match data and solving a linear system, I estimated an offensive power rating for each robot, which my team used to predict match outcomes and choose alliances.

A collection of Flash games I published to the Newgrounds game portal as a teenager.




